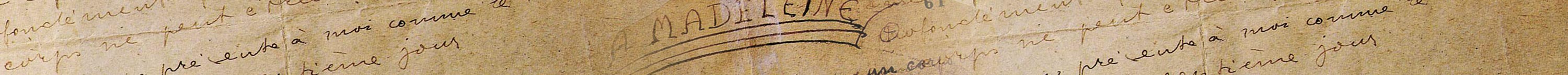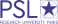01/10/2023 - 30/09/2027

Le projet BANANA financé par l’ANR vise à exploiter et à valoriser les archives du groupe de mathématiciens Nicolas Bourbaki en mobilisant des approches qui se situent au croisement de la génétique des textes, des humanités numériques, ainsi que de l’histoire sociale et conceptuelle des mathématiques.

Fondé en 1934-1935, le collectif connu sous le pseudonyme Nicolas Bourbaki apparaît comme l’un des principaux représentants et promoteurs du structuralisme mathématique en France. Avant tout, Bourbaki est un auteur collectif, seul signataire des Éléments de mathématique, une entreprise éditoriale sur la longue durée couvrant tout un pan des mathématiques pures.

Après la Seconde Guerre mondiale, Bourbaki, qui rassemble des mathématiciens très majoritairement issus de l’élite normalienne, devient l’un des acteurs centraux de la communauté mathématique. Bourbaki jouit par ailleurs d’une progressive reconnaissance internationale, et fait figure de connecteur culturel entre le structuralisme dans les sciences humaines et l’Oulipo dans le champ littéraire.

Les archives Bourbaki, constituées par le groupe lui-même, demeurent quasiment inédites et inexploitées pour la période 1953-1969. Elles sont conservées pour l’essentiel à la bibliothèque de l’Institut Élie Cartan, aux Archives Henri Poincaré, à l’École normale supérieure de la rue d’Ulm et aux Archives de l’Académie des sciences, et ont été partiellement inventoriées par Liliane Beaulieu et Christian Houzel au début des années 2000. On y trouve en particulier les numéros du journal de Bourbaki et des centaines de Rédactions, c’est-à-dire des rapports ou des états intermédiaires documentant la genèse des Éléments. L’hypothèse de départ de BANANA est qu’une étude faisant varier les échelles d’observation sur ce corpus permettra de mieux cerner comment se structure le groupe sur la longue durée tout en analysant finement ses pratiques collectives d’écriture. Pour ce faire, les membres du projet combineront histoires sociale et conceptuelle des mathématiques, articulant deux courants historiographiques, ce qui fait son originalité : d’une part les développements nouveaux de la critique génétique étendue aux textes scientifiques et aux pratiques collectives d’écriture ; et d’autre part les recherches en histoire sociale des sciences et des mathématiques que nous appuierons sur une exploitation qualitative et quantitative d’archives inédites.

Le projet BANANA s’articulera autour de trois objectifs. Un premier axe, au croisement de l’archivistique et des humanités numériques, est d’analyser selon quelles modalités et en fonction de quels choix le groupe Bourbaki a participé à la patrimonialisation de ses propres archives. L’exploitation et à valorisation de celles-ci sera au cœur de cet objectif, et passera par l’enrichissement progressif des Archives numérisées de Bourbaki hébergées de manière coordonnée par Mathdoc et par les Archives Henri Poincaré. Un deuxième axe, articulant histoire et philosophie des mathématiques, vise à mobiliser et développer des méthodes de critique génétique permettant de déplier les processus de fabrication textuelle et conceptuelle des Éléments, tout en attaquant de front les questions historiographiques et épistémologiques que soulèvent les pratiques d’écriture collective de Bourbaki.  Un troisième axe, à l’interface entre l’histoire et la sociologie des sciences, est de poursuivre le travail de réévaluation de la position qu’occupe Bourbaki dans le champ mathématique jusqu’à la fin des années 1960, en montrant notamment en quoi les activités du groupe ont contribué à la disciplinarisation de certaines branches des mathématiques modernes, notamment dans les enseignements de niveau universitaire.

Étapes et objectifs du projet

Axe 1

• Cartographier les fonds, identifier les opérations accomplies par le groupe pour les conserver et les classer.
• Poursuivre la numérisation, le catalogage et l’édition des archives de Bourbaki.
• Sur le site Omeka Classic des Archives Poincaré : versement de nouvelles numérisations, développement de dossiers de genèse de fascicules des Éléments de mathématique, mise au point d’une interface de visualisation pour comparer plusieurs Rédactions.
• Transcrire (manuellement) certaines Rédactions pour une comparaison fine entre différents états d’un chapitre des Éléments ; ajouter un outil de recherche sous forme de glossaire – en collaboration avec la plateforme EMAN (Édition de Manuscrits et d’Archives Numériques, THALIM).
• Expérimenter sur la reconnaissance optique de caractère (OCR), participer aux efforts développés autour de l’exploration sur la reconnaissance automatique des caractères et des formules mathématiques (collaborations déjà engagées avec EMAN et le projet ERC PHILIUMM).

Axe 2

• Reconstituer la genèse de livres ou de chapitres des Éléments de mathématique
• Développer et repenser les études génétiques pour les textes mathématiques, voire au-delà. Identifier, explorer et confronter les différents angles d’attaque auxquels se prête le Bourbaki corpus en termes de critique génétique.
• Proposer des études de cas combinant genèse textuelle, genèse conceptuelle et socio-genèse, en interrogeant en particulier les dynamiques d’écriture collective.
• Réexaminer le structuralisme de Bourbaki en nous appuyant sur des corpus de Rédactions, et, par là, montrer en quoi réflexions épistémologiques et critique génétique s’éclairent mutuellement.
• Enrichir les travaux historiques et philosophiques sur le structuralisme de Bourbaki en clarifiant comment certaines structures mathématiques ont été introduites, définies et classées.
• Analyse du poids relatif exercé par certaines valeurs épistémiques (e.g., généralité, pureté de méthodes) dans les stratégies d’écriture adoptées par certains membres du groupe.

Axe 3

• Présenter une étude socio-historique du groupe enrichissant les précédentes contributions sur le sujet, en nous appuyant sur des méthodes prosopographiques qui ont déjà fait toute la preuve de leur fécondité en étant appliquées à une échelle microhistorique.
• Proposer des analyses de séquences (avec le logiciel TraMineR) permettant de repérer des types de trajectoires parmi les rédacteurs des Éléments de mathématique.
• Mesurer l’impact qu’a eu l’appartenance à Bourbaki sur les carrières de ses membres.
• Déterminer dans quelle mesure les activités de Bourbaki ont contribué à ce que certaines branches des mathématiques centrées sur l’étude de structures se disciplinarisent.
• Examiner les usages savants et académiques qui ont pu être faits des fascicules des Éléments de mathématique.
• Mettre en valeur certains réseaux d’acteurs ayant contribué à la singulière notoriété internationale des Éléments de mathématique.

 

Participant.e.s

Équipe Archives Henri Poincaré

ECKES Christophe (Coordinateur)

ARANA Andrew

BETTAHAR Yamina

BRUNEAU Olivier

HEINZMANN Gerhard

ROLLAND Camille

ROLLET Laurent

ROCHER Mélusine

WILLAIME Pierre

AFGOUSTIDIS Alexandre

BRECHENMACHER Frédéric

PEYRE Emmanuel

REMMERT Volker

REMY Bertrand

RICOTIER Gatien

VERSCHUEREN Pierre

 

Équipe ITEM

HAFFNER Emmylou (Coordinatrice)

CANTÙ Paola

CHORLAY Renaud

KRÖMER Ralf

MONTÉMONT Véronique

PATRAS Frédéric

WALTER Richard

WASZEK David

ZACCARELLO Benedetta

L’équipe de la cellule Mathdoc

---

Descriptif du projet sur le site de l’ANR